由图3可知,低频部分为原始功率曲线的主导部分,其幅值与原始功率信号相近,可以对原始功率信号的概貌进行描述,高频部分则能量较小,且在零值附近上下波动,幅值明显小于低频部分,因此,将低频信号作为并网功率参考值,采用小波包分解滤波方式得到风电功率平滑曲线如图4所示。
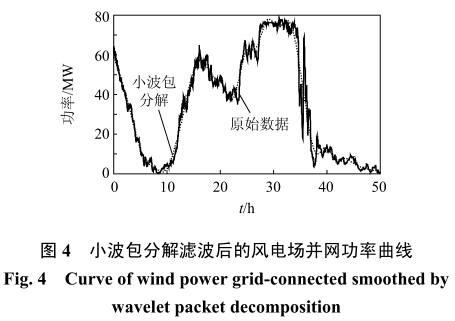
由图4可知,经小波包分解滤波后得到的风电功率曲线波动大幅降低,可以快速地跟踪储能系统的输入目标值,获得更平滑的输出功率,不存在滞后现象。由于经小波包分解后接入储能系统的信号仅为高频信号,其幅值小且在零值附近上下波动。但是由图3中次高频和最高频部分可知,虽然其都是围绕零值上下波动的随机信号,但是其幅值大小具有明显差别,数量级差别达到103。根据高频信号的这一特点及蓄电池的响应速度可知:如果采用单一的蓄电池储能方式吸收其高频部分,不仅无法实现小波包分解功率平衡的需求,而且频繁的充放电动作将会对储能电池的寿命造成很大的影响。因而,对高频信号中次高频及最高频部分分别选用不同的储能方式来平抑风电场输出功率的波动。
1.3基于混合储能技术的风电场输出功率平滑控制
风电场输出功率信号通过小波包分解得到的低频信号由于其能量高变化慢起主导作用,将之作为期望的并网功率值,而高频信号能量低变化快,则由储能系统进行吸收以达到平滑功率输出的目的。考虑到储能电池具有能量密度高和功率密度、循环使用寿命低等特点,将次高频信号由电池储能系统进行平滑;而超级电容器具有功率密度高、循环寿命高和能量密度低等特点,将未被电池储能系统平滑掉的功率信号及其它高频信号送往超级电容器进行快速滤波处理。根据这一思想,按照文献[19]选择电池响应时间为1h,其响应频率为2.78×10−4Hz,与经小波包分解后得到的S8,1—S8,4次高频信号响应频率几乎一致,因此选择电池储能系统吸收该段频率信号;剩余的高频信号S8,5—S8,255及未被电池吸收部分均由超级电容器吸收,实现风电功率平滑的目的,其功率平滑控制框图如图5所示。
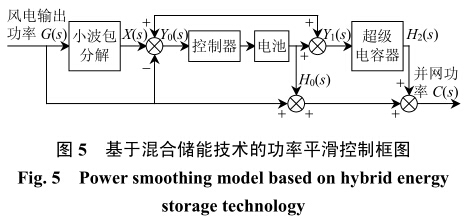
由图5可知,当风电场实际有功功率G(s)大于小波包分解给出的预期功率X(s)时,对电池储能系统和超级电容器发送充电指令;当风电场实际有功功率G(s)小于小波包分解给出的预期功率X(s)时,对电池储能系统和超级电容器发送放电指令。