在充放电过程中,由于电池惯性大并且响应速度慢,电池的实际输出H0(s)并不完全等于目标值Y0(s),电池储能系统只对次高频部分进行了吸收,而剩余的最高频部分及未由电池储能系统吸收的部分则由超级电容器完成吸收。当电池输出与超级电容器输出H0(s)+H1(s)=Y0(s)时,实际的并网功率C(s)等于预期的并网功率X(s),功率平滑过程结束。
2小波包分解在混合储能平抑风电功率波动中的应用
2.1两种储能方式下的功率平滑效果对比
根据1.1节中给出的风电场全年输出功率数据,分别采用单类型电池储能和电池与超级电容混合储能两种储能方式对经小波包分解后的高频信号进行吸收,其功率平滑曲线如图6所示。
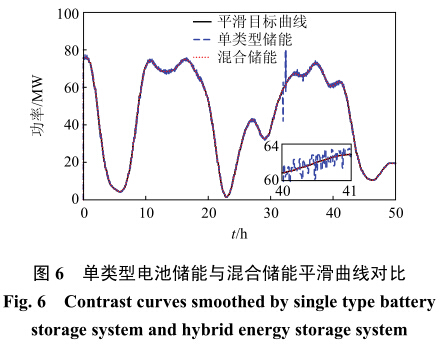
由图6可以看出,通过混合储能方式对高频信号进行吸收可以得到更加平滑的输出曲线,且对目标功率跟踪较好,曲线几乎重合,而使用单类型电池储能得到的平滑效果则不是很理想,曲线毛刺较多,效果较差(如图6中放大部分)。为了进一步比较单类型电池储能及混合储能的平滑效果,图7给出了在两种储能方式下输出功率与目标功率的误差曲线。
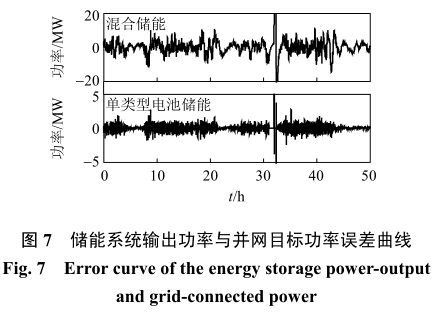
由图7可知,在给定相同的目标功率值情况下,经单类型电池储能系统吸收后,其输出功率与目标功率的差值在±5MW之间波动;而经混合储能系统吸收后,其输出功率与目标功率的差值则在±10kW之间波动,远远小于单类型电池储能系统。
根据文献[20]给出的储能容量计算公式得到在两种储能方式下50h内所需配置的最大储能容量为21.21MW⋅h,考虑到电池的使用寿命及20%的裕度,拟配置25MW⋅h。由上文可知,输入到电池的信号为次高频部分,剩余高频部分输入到超级电容器中,对滤波能量进行频谱分析,得到次高频部分与高频部分的能量比为623:2,依据该能量比配置电池储能系统容量为24.92MW⋅h,超级电容器容量为0.08MW⋅h,其储能容量变化曲线如图8所示。